广度优先搜索
简介
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止
相关概念
广度优先搜索的运行时间为O(顶点 + 边数),这通常写作O(V + E),其中V为顶点(vertice)数,E为边数
对于检查过的人(顶点),务必不要再去检查,否则可能导致无限循环
主要步骤
- 使用图来建立问题模型
- 使用广度优先搜索解决问题
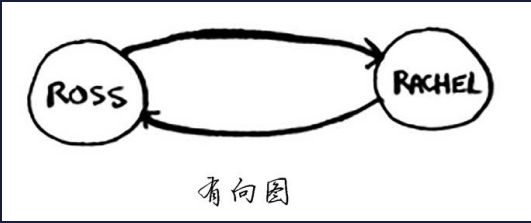
有向图、无向图
有向图是单向的
无向图没有箭头,直接相连的节点互为邻居,无向图相邻的两个结点彼此指向对方,其实就是一个环,跟上图一样
实操
有这么一个人员数据表,他们都有各自的职业和邻居,假设你是其中一个人:a——工地搬砖工。有一天,你想吃新鲜的蔬菜,但是你不相信陌生人,所以你打算问你的邻居,看看有没有什么认识的人(职业为农民)可以提供保证新鲜的蔬菜给你,如何操作呢(下面为思路)
1 | let obj = { |
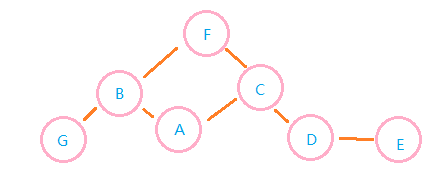
根据广度优先搜素算法,我们首先根据各个人员的邻居构建出图模型
接着就是从你(a)自己入手,首先你从b和c开始找起,如若b和c就是农民,那么久返回该对象的名字,我们可以将这两人压入待查找数组
1 | [b,c]; |
b如果不是,那么就把b的邻居加入数组,一起找
1 | [b,c,a,f,g]; |
同时把b弹出
1 | [c,a,f,g]; |
当然,a也不是,否则查找会造成循环,不断去找a,所以一开始我们需要定义一个数组用以存储已查过的对象,然后每次查完一个放进一个,后面的每次查找待找数组时在已查找数组中查看是否已查过,是则把该值从待找数组中丢掉
1 | let finded = ['a']; |
继续上面几个步骤,对后面的数据进行查找↓
接下来是c,c也不是,所以把c的邻居也加进来
1 | [a,f,g,a,f,d]; |
重复这几个步骤,直到找出最终的结果
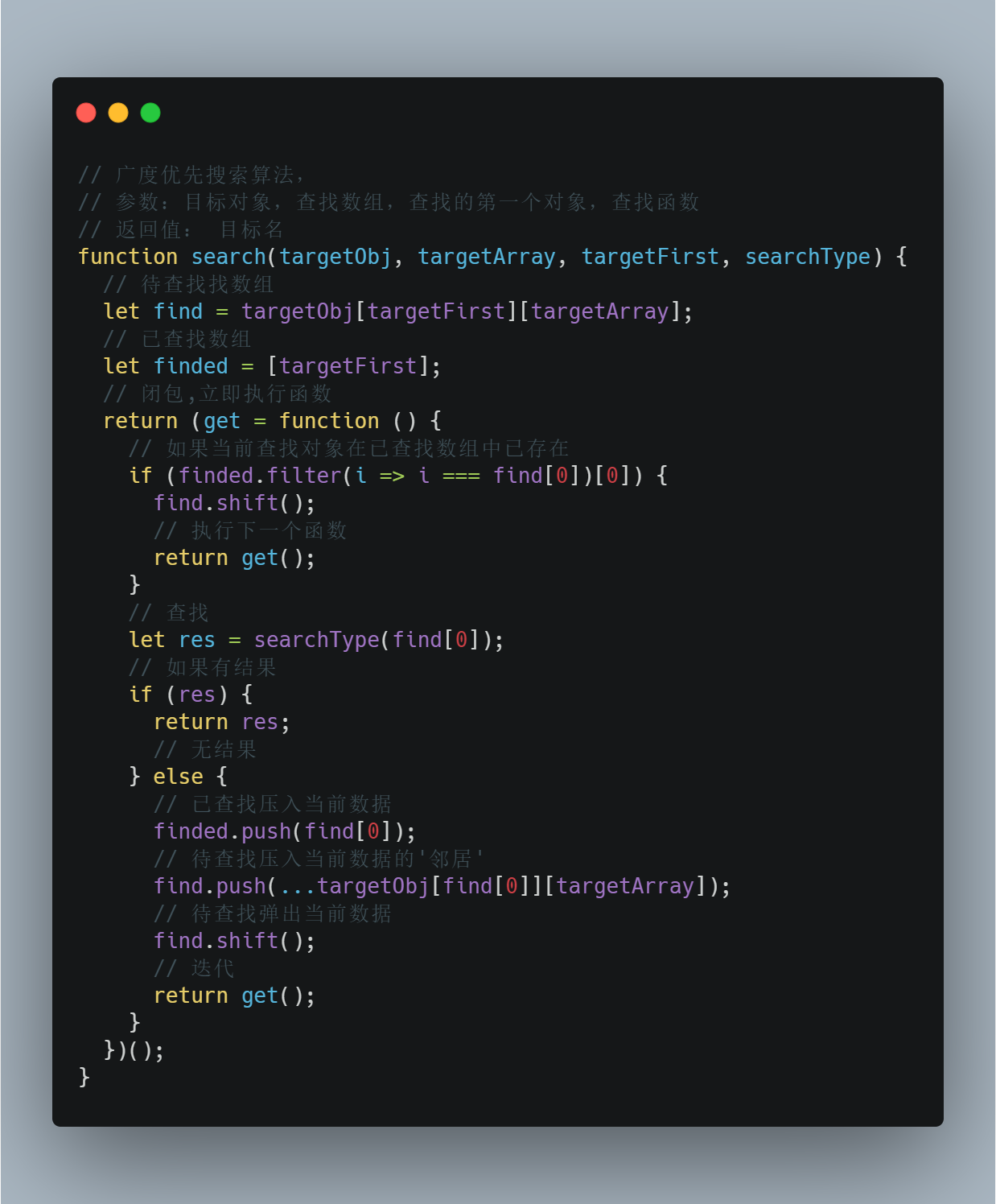
方法代码如下
总结
- 广度优先搜索指出是否有从A到B的路径。
- 如果有,广度优先搜索将找出最短路径。
- 面临类似于寻找最短路径的问题时,可尝试使用图来建立模型,再使用广度优先搜索来 解决问题。
- 有向图中的边为箭头,箭头的方向指定了关系的方向,例如,rama→adit表示rama欠adit钱。
- 无向图中的边不带箭头,其中的关系是双向的,例如,ross - rachel表示“ross与rachel约 会,而rachel也与ross约会”。
- 队列是先进先出(FIFO)的。
- 栈是后进先出(LIFO)的。
- 你需要按加入顺序检查搜索列表中的人,否则找到的就不是最短路径,因此搜索列表必 须是队列。
- 对于检查过的人,务必不要再去检查,否则可能导致无限循环。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Dong!
评论