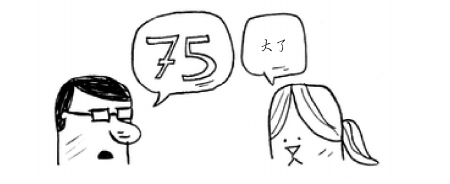二分法

简介

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

算法过程

首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功

简单查找

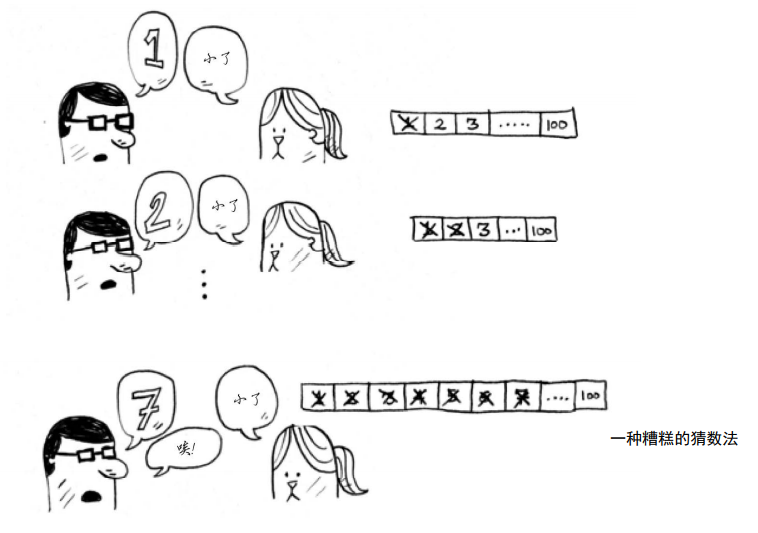
我们在日常生活中经常会玩一个游戏：找数字

提问者给出该数字的范围，然后回答者根据这个范围进行猜数，如果比正确答案大，提问者便会说大了，如若小了，则提问者回答小了，直至猜出正确答案

比如：提问者随便想出一个数字-57，范围是0-100，回答者开始猜，如下图

等到他猜到57，便成功猜到正确答案了，这便是简单查找，回答者一个一个说，直到正确答案出来

二分查找

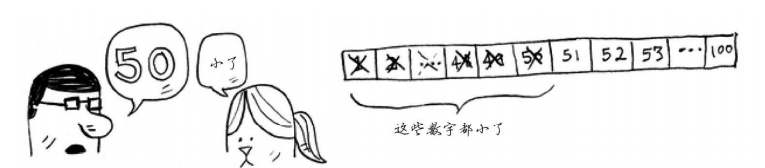
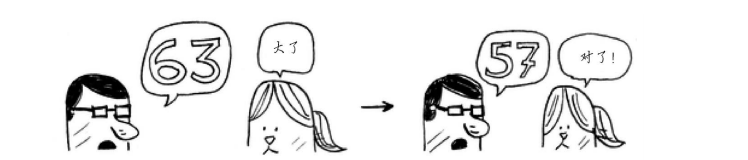
更简单的查找方式，根据方法名即可猜到，将猜测范围一分为二，比如0-100，那么你猜50，无论是大了还是小了，你立即就可以排除掉一半的数字，接着重复一分为二的操作进行猜数，最后得出正确答案

梳理下这个猜数的过程，我们一共进行了几步

回过头去，如果你采用暴力式简单查找，那么你猜的数字便是n（答案n）步，如果目标数字小，还好，如果是99呢，你就得猜到99才能猜到

引用书籍的另一个例子——

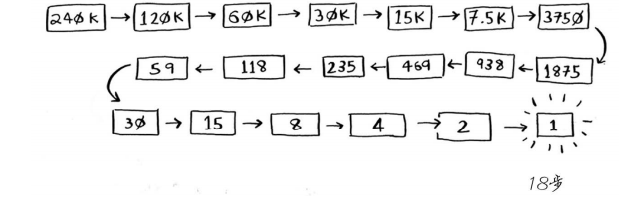
假设你要在字典中查找一个单词，而该字典包含240 000个单词， 你认为每种查找最多需要多少步？ 如果要查找的单词位于字典末尾，使用简单查找将需要240 000步。使用二分查找时，每次排除一半单词，直到最后只剩下一个单词。

可见，随着要猜的范围越来越大，二分查找的优势也越加凸显，而二分查找所需的步数也符合对数的规律

二分查找最多需要log2n步

代码实现

简单查找

我们首先看简单查找的代码实现（这里包括后面只会给出图片格式的代码，因为更多的希望通过实操去理解每个算法的过程）

直接通过遍历，一个一个判断，最后返回结果

二分查找

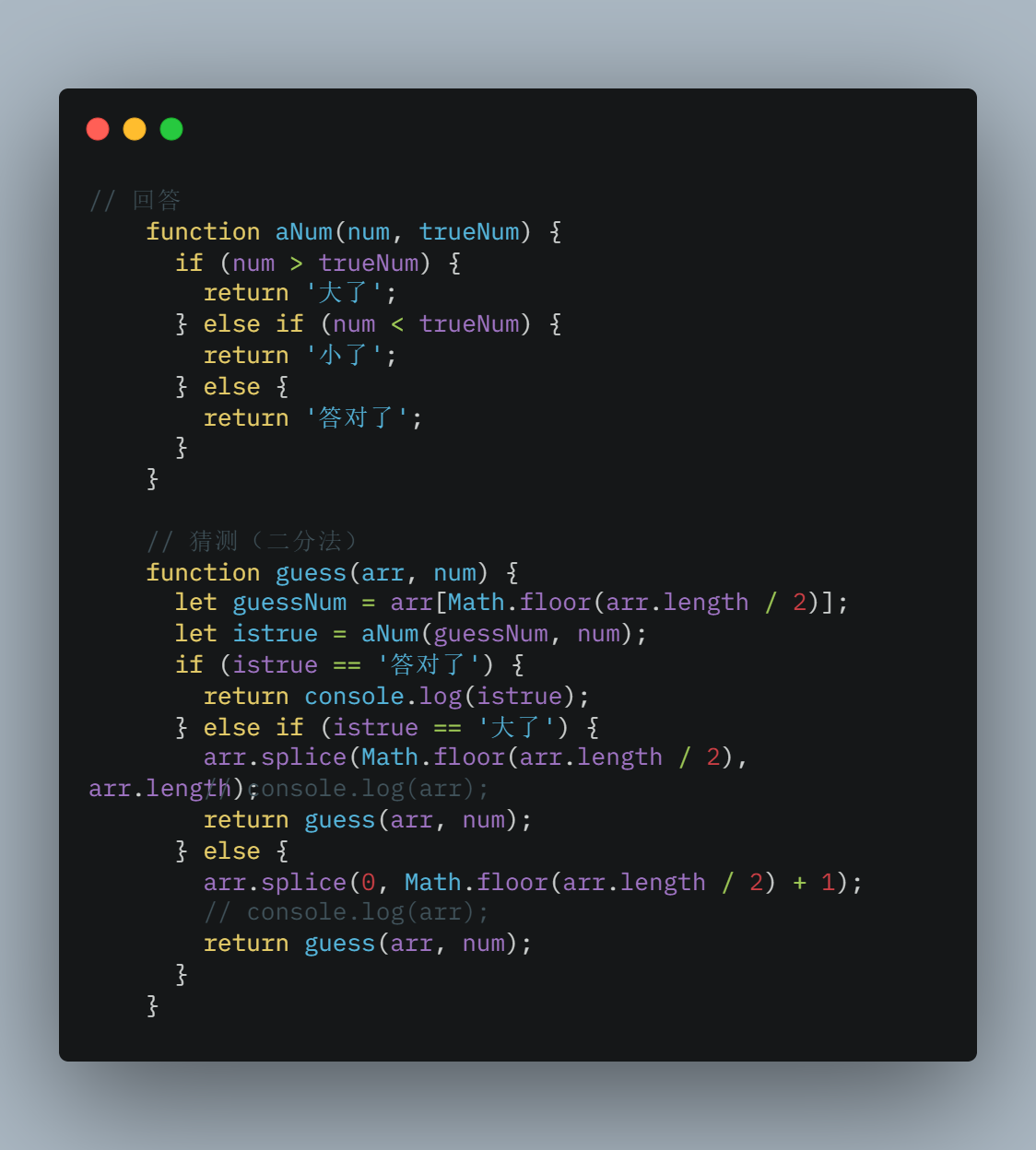
看看二分查找的实现代码（因为是根据自己的理解所写，所以多多少少可能会有不合理的地方，望指出）

1. 首先是写一个回答函数，相当于提问者的回答，传入参数包括回答者的数字和正确的数字
2. 接着便是使用二分法进行猜数，每次猜中间数，对了返回，不对就根据情况进行数组裁剪，裁剪完继续重复该函数（递归思想）

总结

O(log n)比O(n)快（也就是二分法比简单查找快），当需要搜索的元素越多时，前者比后者快得越多