简介

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。

我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式

背包问题

image-20220221172703812

image-20220221180313039

解决方式就是采用动态规划

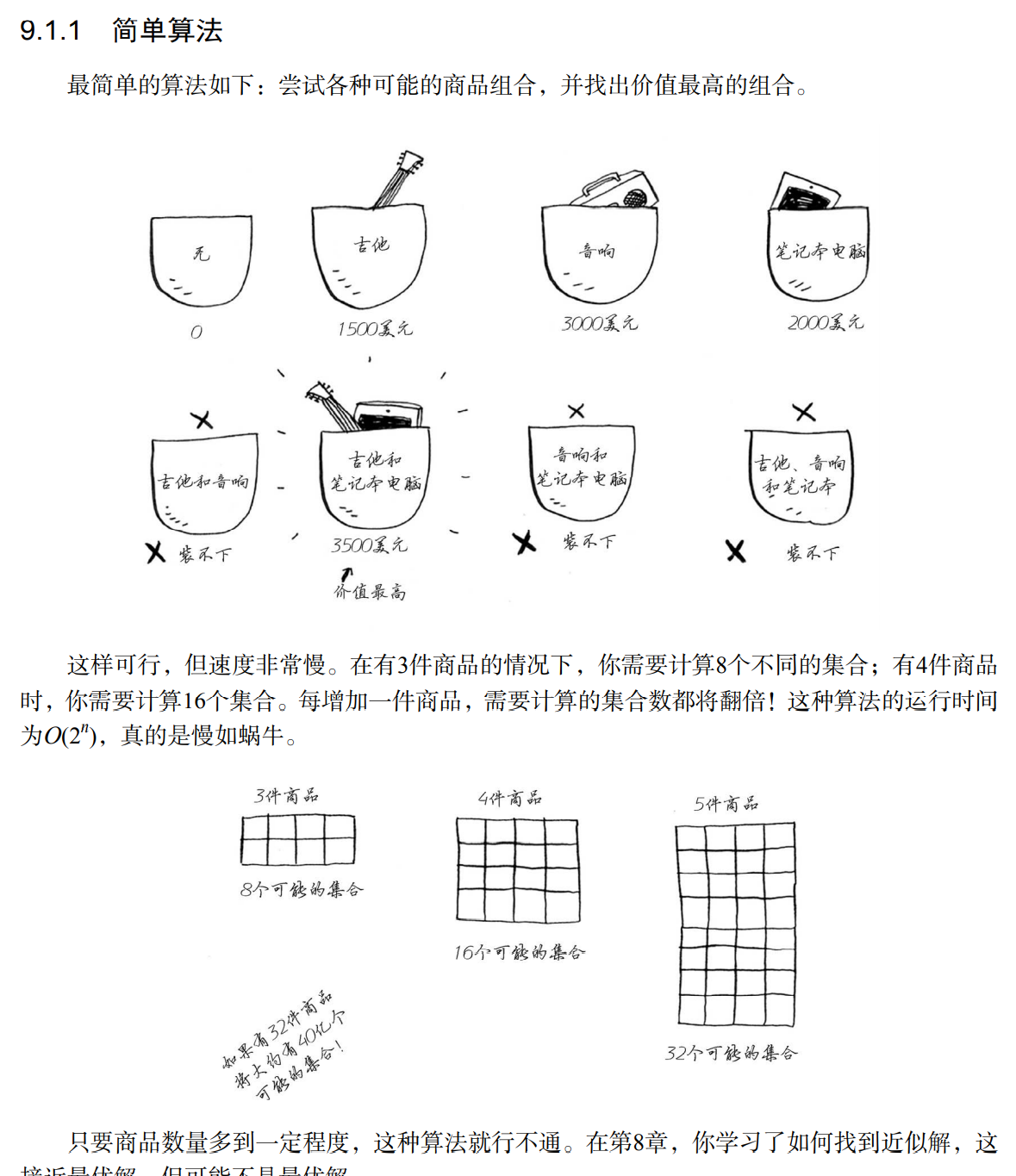
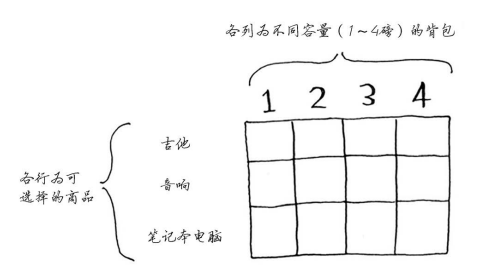
image-20220221180638182

背包分割的最小重量取决于能拿的最小物品重量，如果此时最小物品为0.5，那么背包就要被划分成4/0.5 = 8，8列

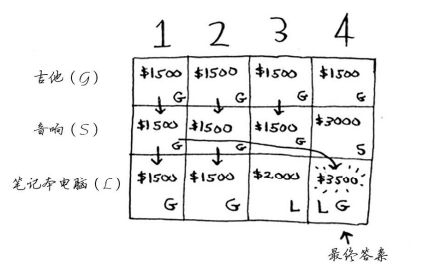
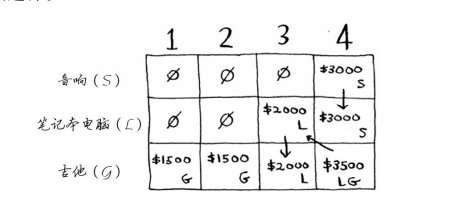
在每一行， 可偷的商品都为当前行的商品以及之前各行的商品，逐行进行计算，比如第一行，可拿的物品只有吉他，那么接下来四格，就都只能考虑吉他，所以全都填充为单个吉他的价值，等到第二行时，可选的选项就有音响和前一行的吉他了，这时候每个单元格再根据物品价值和质量综合判断来进行数据填充，音响重量有4，所以前面依旧沿用吉他的价值，直接到音响的重量所处格子，这时候我们发现音响价值在4的时候大于1500，也就是音响本身价值大于吉他，所以进行替换，接下来亦是如此，到第三行第四个格子我们发现笔记本电脑的价格加上上一行4-笔记本重量所处单元格的价值大于上一行4所处价值，所以得出最终的结果

计算结果如下

image-20220221180723661

计算每个单元格的价值时，使用的公式如下

在1和2之间进行比较，选择大的那方

image-20220221182208929

注意点

  1. 各行的排列顺序无关紧要

    也就是说哪个物品先判断都行，你想把音响放在最开始进行分析都可以，不影响结果（但在后面的代码中为了方便我还是会为数据进行排序，从最轻的拿起，可以思考下我为什么那样做，当然也有可能会是我想不到（不足）的地方（怕打脸哈哈哈））

    image-20220221183039104

  2. 使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分（你只能把它当作一个最小的整体，不能继续分割的整体）

    如果想处理像偷大米、黄豆之类可以拆出来倒到背包的问题时，则可以使用贪婪算法

    image-20220221183404146

  3. 相互依赖的情况

    没办法建模。动态规划功能强大，它能够解决子问题并使用这些答案来解决大问题。但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。这意味着使用动态规划算法解决不了子问题会相互产生影响的问题

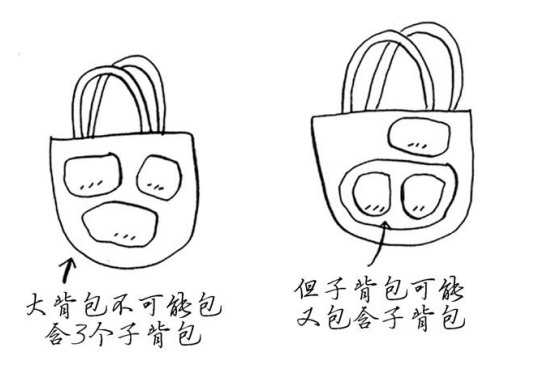
  4. 为获得前述背包问题的最优解，可能需要偷两件以上的商品。但根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包

    形象来说就是一分为二，再在每个子背包中一分为二（有点类似二叉树）

    image-20220221183745856

  5. 最优解可能会导致背包没装满

    假设你还可以偷一颗钻石。 这颗钻石非常大，重达3.5磅，价值100万美元，比其他商品都值钱得多。 你绝对应该把它给偷了！但当你这样做时，余下的容量只有0.5磅，别的什么都装不下

代码

思路如下

  1. 因为从上面的算法得出：每次计算当前行都只会用到上一行的数据，所以我并没有像书里一样使用表格去记录这个过程，我使用了两个二维数组prices、goods分别用来存储每格的价值和所含物品，每次每行计算后的最新结果goods[1]会重新赋值给goods[0]，计算前又将goods[0]默认赋值给goods[1]，这样就可以只在价格有改变时改变单元格即可， prices同理
  2. 然后对初始数据initData进行排序，这样可以保证最开始那一行是有数据的，如果是别的比较重的物品，则最开始那几个空格就会为空，就又要去做一些多余的判断或者赋默认值，挺麻烦的，怕代码冗余和出现一些问题
  3. 内层（列）遍历，每次都只用从当前物品重量对应单元格开始算，毕竟前几格你也放不下嘛，默认当前格的上一行值即可，减少代码判断
  4. 核心判断语句不变，跟上面一致
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
// 深拷贝函数
function copyDeep(data) {
  return JSON.parse(JSON.stringify(data));
}

//算法
function dynamicToGetGoods(data, bagWeight) {
  let initData = Array.from(data); //数据初始化，防止修改到原数据
  let prices = [[], []]; //存放价值的数组
  let goods = [[], []]; //存放每个最大价值所含物品
  initData.sort((a, b) => a.weight - b.weight); //数据初始化排序，从小到大
  let baseWeight = initData[0]['weight']; //获得基础容量
  let pricesLength = Math.floor(bagWeight / baseWeight); //获得背包应分割的数量,向下取整，排除书包额外容量

  // 初始化数据,相当于遍历第一件商品
  for (let i = 0; i < pricesLength; i++) {
    prices[0].push(initData[0]['price']);
    goods[0].push([initData[0]['name']]);
  }
  // 删除当前商品，避免参与下面的算法执行
  delete initData[0];

  // 算法核心，从第二件商品开始遍历，对每一件商品进行数据填充
  for (const key in initData) {
    const element = initData[key];
    let elementWeightIndex = element['weight'] / baseWeight - 1; //物品重量对应索引

    prices[1] = copyDeep(prices[0]); //默认从上一行取值
    goods[1] = copyDeep(goods[0]); //默认从上一行取值

    for (let i = elementWeightIndex; i < pricesLength; i++) {
      //第一种情况：当前物品重量同当前背包小格重量相等
      if (i == elementWeightIndex) {
        // 如果当前物品价格大于先前价格
        if (element['price'] > prices[0][i]) {
          // 赋值为当前物品及价格
          prices[1][i] = element['price'];
          goods[1][i] = [element['name']];
        } 

        // 第二种情况，当前物品重量大于当前背包小格重量
      } else if (i > elementWeightIndex) {
        // 如果当前物品价格加上（当前背包质量-当前物品质量）的价格大于先前价格
        if (element['price'] + prices[0][i - elementWeightIndex - 1] > prices[0][i]) {
          // 赋值为当前物品和（当前背包质量-当前物品质量）的物品总和及价格总和
          prices[1][i] = element['price'] + prices[0][i - elementWeightIndex - 1];
          goods[1][i] = [element['name'], ...goods[0][i - elementWeightIndex - 1]];
        }
      }
    }
    prices[0] = copyDeep(prices[1]);
    goods[0] = copyDeep(goods[1]);
  }

  return {
    goods: goods[1][pricesLength - 1],
    price: prices[1][pricesLength - 1],
  };
}

运行下

模拟数据有点多，不要介意，确保可靠嘛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
let data = [
  { name: '吉他', price: 1500, weight: 1 },
  { name: '音响', price: 3000, weight: 4 },
  { name: '笔记本电脑', price: 2000, weight: 3 },
  { name: 'iphone', price: 2000, weight: 1 },
  { name: 'ipad', price: 2000, weight: 2 },
  { name: '自行车', price: 50000, weight: 15 },
  { name: '钻石', price: 50000, weight: 3 },
  { name: '花', price: 50, weight: 0.5 },
  { name: '巧克力', price: 500, weight: 0.5 },
  { name: '耳机', price: 1500, weight: 0.5 },
];

let res = dynamicToGetGoods(data, 10);
console.log(res);

结果：

1
{ goods: [ '音响', '钻石', 'iphone', '吉他', '耳机', '巧克力' ], price: 58500 }

算法思路

  1. 动态规划可帮助你在给定约束条件下找到最优解。在背包问题中，你必须在背包容量给定的情况下，偷到价值最高的商品。
  2. 在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。
  3. 每种动态规划解决方案都涉及网格
  4. 单元格中的值通常就是你要优化的值。在前面的背包问题中，单元格的值为商品的价值。
  5. 每个单元格都是一个子问题，因此你应考虑如何将问题分成子问题，这有助于你找出网格的坐标轴

每次用的时候问问自己

  1. 单元格中的值是什么？
  2. 如何将这个问题划分为子问题？
  3. 网格的坐标轴是什么？

算法步骤

  1. 建立表格
  2. 确定每一个格的值代表什么
  3. 如何将大问题划分为具有相同解法的子问题
  4. 确定网格坐标轴

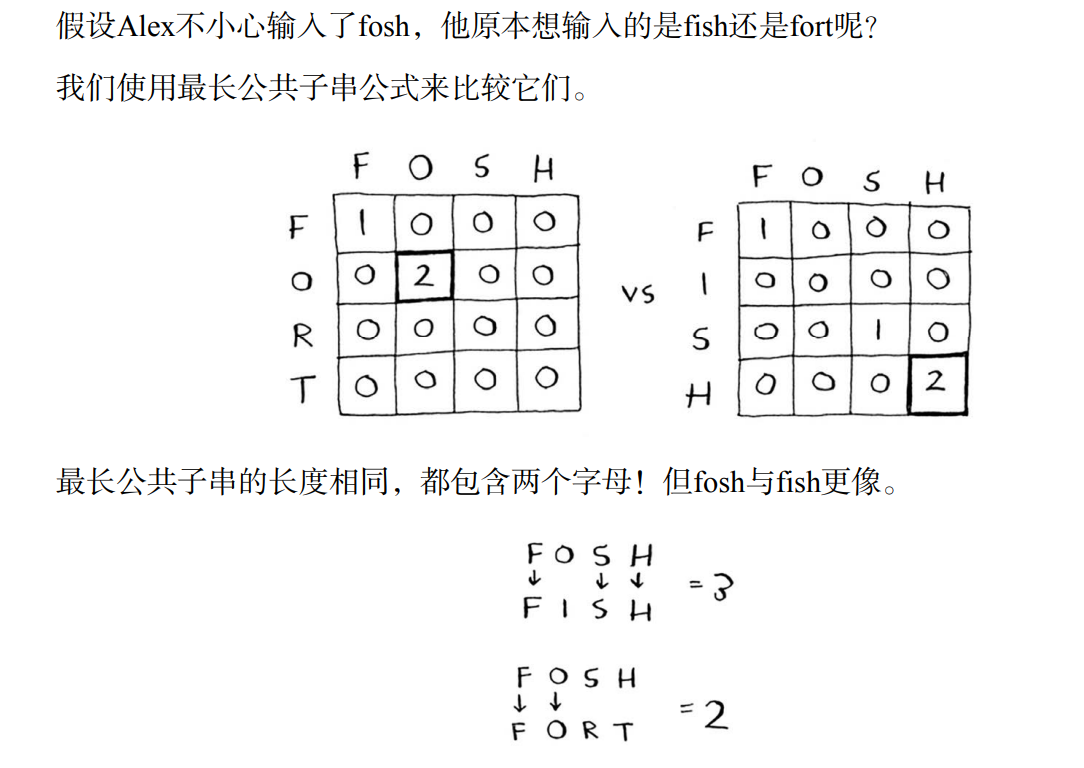
最长公共子串

image-20220221185431847

尝试一下，在纸上绘制网格，将每个单词分解（子问题）

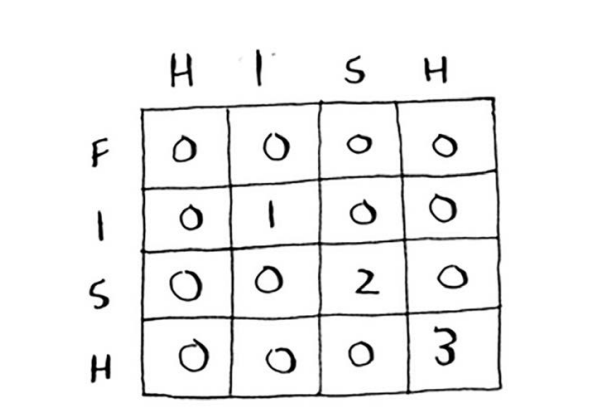
答案如下（思考下，这是如何得出的）

image-20220221185929563

解决这个问题核心的伪代码类似于下面这样

image-20220221185552675

注意！！！

  1. 对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中

    image-20220221190054121

代码

你可以先尝试着根据上面的思路自己写一下

在写的过程中你是否会发现一个问题，在代码的实现上，我们会发现上面的公式会有些问题，毕竟我们是用二维数组去记录这个过程，所以某些情况下会出现data[index1 - 1][index2 - 1]报错的情况，什么情况下呢

如下图，这些情况下的值在你按部就班时运行会报错的，因为它缺少斜对角的值，毕竟没有data[-1][-1]这样的值出现

image-20220222085726502

怎么解决，有两种方法，第一种是每次到该计算都做一下判断，判断是否有值，我嫌太麻烦了，且影响从代码上去理解这个算法的思路，所以使用第二种，给你一个二维数组，你就会理解了，然后我就懒得解释了哈哈哈

1
2
3
4
5
6
7
[
  [ 0, 0, 0, 0, 0 ],
  [ 0, 0, 0, 0, 0 ],
  [ 0, 0, 1, 0, 0 ],
  [ 0, 0, 0, 2, 0 ],
  [ 0, 1, 0, 0, 3 ]
]

在里面，我会用一个函数fillDataByWordLength去填充第一行的0，以及在内层循环（列）中每次一开始填充一个0

还有一点，我使用了max和maxWord在每次判断时去分别存储最长公共子串长度和最长公共子串，免得后面再在二维数组去找一个最大值

1
data[index1][index2] > max && ((max = data[index1][index2]), (maxWord1Position = index1 - 1)); //最长公共子串数赋值

getMaxWord函数主要用作获得最长的公共子串，比如，fish和fosh最长的公共子串就为sh

然后再看看下面的代码，应该没啥问题了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 根据word长度填充数组
function fillDataByWordLength(word, data) {
  let arr = [];
  for (let i = 0; i <= word.length; i++) {
    arr.push(data);
  }
  return arr;
}

// 获得最长的公共子串
function getMaxWord(word, maxWordPosition, max) {
  let res = '';
  for (let i = maxWordPosition - max + 1; i <= maxWordPosition; i++) {
    res += word[i];
  }
  return res;
}

// 动态规划
function dynamicToGetCommonWords(word1, word2) {
  let data = []; //存储动态规划网格
  let max = 0; //存储最长公共子串数
  let maxWord; //存储最长公共子串
  let maxWord1Position; //存储最长公共子串截至位置
  data[0] = fillDataByWordLength(word2, 0); //数组填充

  // 算法核心
  for (let index1 = 1; index1 < word1.length + 1; index1++) {
    const element1 = word1[index1 - 1]; //获取当前字母
    data[index1] = []; //初始化数组
    data[index1].push(0); //默认第一位为0

    for (let index2 = 1; index2 < word2.length + 1; index2++) {
      const element2 = word2[index2 - 1]; //获取当前对比字母

      if (element1 == element2) {
        // 若相等，则当前单元格值等于左对角线方格值加上1
        data[index1][index2] = data[index1 - 1][index2 - 1] + 1; //当前单元格赋值
        data[index1][index2] > max && ((max = data[index1][index2]), (maxWord1Position = index1 - 1)); //最长公共子串数赋值
      } else {
        // 不相等则赋值为0
        data[index1][index2] = 0;
      }
    }
  }

  maxWord = getMaxWord(word1, maxWord1Position, max);
  return { max, maxWord };
}

运行下

1
2
let res = dynamicToGetCommonWords('fish', 'fosh');
console.log(res);

结果：

image-20220221190426458

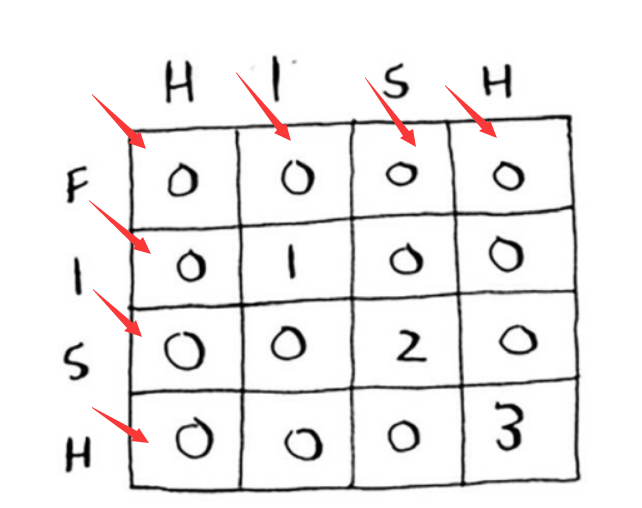
最长公共子序列

image-20220221190516948

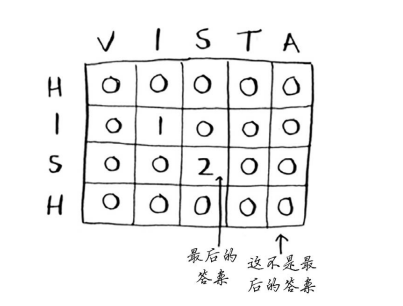
这里比较的是最长公共子串，但其实应比较最长公共子序列：两个单词中都有的序列包含的 字母数。如何计算最长公共子序列呢

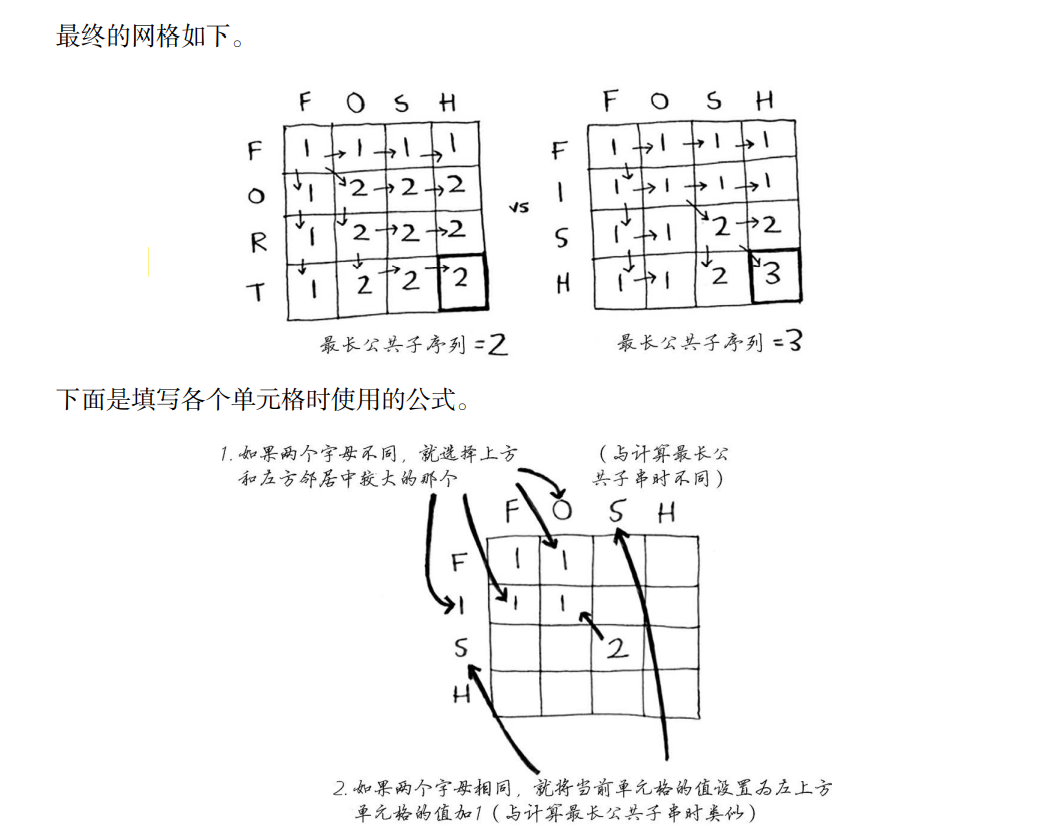
计算过程如下：图很重要！！！！！！（懒得打字了）

image-20220221190615957

核心伪代码

image-20220221190713163

代码

思路是和上面例子很相近的，只是判断语句不同了而已，直接看代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 根据word长度填充数组
function fillDataByWordLength(word, data) {
  let arr = [];
  for (let i = 0; i <= word.length; i++) {
    arr.push(data);
  }
  return arr;
}

// 动态规划
function dynamicToGetCommonWords(word1, word2) {
  let data = []; //存储动态规划网格
  data[0] = fillDataByWordLength(word2, 0); //数组填充

  // 算法核心
  for (let index1 = 1; index1 < word1.length + 1; index1++) {
    const element1 = word1[index1 - 1]; //获取当前字母
    data[index1] = []; //初始化数组
    data[index1].push(0); //默认第一位为0

    for (let index2 = 1; index2 < word2.length + 1; index2++) {
      const element2 = word2[index2 - 1]; //获取当前对比字母
      if (element1 == element2) {
        // 若相等，则当前单元格值等于左对角线方格值加上1
        data[index1][index2] = data[index1 - 1][index2 - 1] + 1; //当前单元格赋值
      } else {
        // 若不相等，则从左边或上边的邻居方格中取一个最大值
        data[index1][index2] = Math.max(data[index1][index2 - 1], data[index1 - 1][index2]);
      }
    }
  }
  return { res: data[word1.length][word2.length], calculationMatrix: data };
}

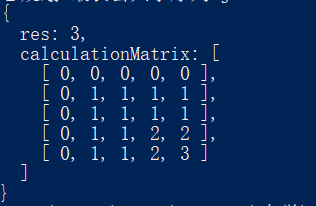
运行下

1
2
let res = dynamicToGetCommonWords('fish', 'fosh');
console.log(res);

结果：

image-20220221191104618

小结

动态规划的实际应用

  • 生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。
  • 你使用过诸如git diff等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。
  • 前面讨论了字符串的相似程度。编辑距离（levenshtein distance）指出了两个字符串的相似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否是盗版，都在其中。
  • 你使用过诸如Microsoft Word等具有断字功能的应用程序吗？它们如何确定在什么地方断字以确保行长一致呢？使用动态规划！

总结

  1. 需要在给定约束条件下优化某种指标时，动态规划很有用。
  2. 问题可分解为离散子问题时，可使用动态规划来解决。
  3. 每种动态规划解决方案都涉及网格。
  4. 单元格中的值通常就是你要优化的值。
  5. 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。
  6. 没有放之四海皆准的计算动态规划解决方案的公式