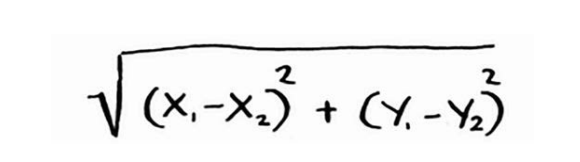K最近邻算法KNN
简介
KNN(K- Nearest Neighbor)法即K最邻近法,最初由 Cover和Hart于1968年提出,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路非常简单直观:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别
该方法的不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最邻近点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。另外还有一种 Reverse KNN法,它能降低KNN算法的计算复杂度,提高分类的效率
KNN算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分
算法步骤
- 准备数据,对数据进行预处理 。
- 计算测试样本点(也就是待分类点)到其他每个样本点的距离
- 对每个距离进行排序,然后选择出距离最小的K个点
- 对K个点所属的类别进行比较,根据少数服从多数的原则,将测试样本点归入在K个点中占比最高的那一类
特征抽取
使用毕达哥拉斯公式计算A和B的相似性(距离),值越小,相似性越大
回归
代码
原理上挺简单的,所以没解释,直接上代码,包含两个函数,一个毕达哥拉斯公式,一个KNN算法
1 | // 毕达哥拉斯 Math.sqrt((x1-x2)² + (y1 - y2)²) |
模拟数据以及测试
1 | // test |
结果
1 | { |
机器学习
小结
- KNN用于分类和回归,需要考虑最近的邻居。
- 分类就是编组。
- 回归就是预测结果(如数字)。
- 特征抽取意味着将物品(如水果或用户)转换为一系列可比较的数字。
- 能否挑选合适的特征事关KNN算法的成败
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Dong!
评论